Abstract
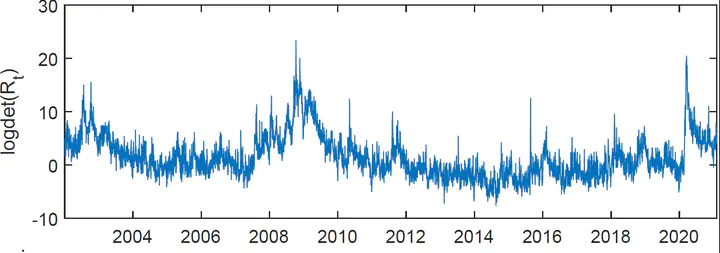
Realized covariance matrices (RCs) are an important input to asses the risks involved in different investment allocations and it is thus useful to model and forecast them. To this end generalized autoregressive score (GAS) models are employed in this paper. These models are ideal for comparing different probability distributions in terms of their ability to model and forecast RCs, since the dynamic parameters of the conditional observation density are updated by incorporating the shape of the distribution itself (via the scaled score of the log-likelihood). All probability distributions so far applied to time series of RCs in the literature are considered. The necessary inputs for the GAS models (Fisher information matrix and score) are derived for all distributions. An in-sample fit comparison confirms previous results that “fat-tailed” distributions outperform others and shows that the novel distribution family achieves very good fit. Out-of-sample forecasting comparisons further corroborate the excellent performance of the novel distribution family.
Michael Stollenwerk
Investment Risk Analyst
Investment Risk Analyst; enhancing the decisions of investment teams by providing quantitative analyses.